Emulation
p
We may regard the present state of the universe as the effect of its past and the cause of its future. An intellect which at a certain moment would know all forces that set nature in motion, and all positions of all items of which nature is composed, …
… if this intellect were also vast enough to submit these data to analysis, it would embrace in a single formula the movements of the greatest bodies of the universe and those of the tiniest atom; for such an intellect nothing would be uncertain and the future just like the past would be present before its eyes.
— Pierre Simon Laplace (Laplace, 1814)
Game of Life
Loneliness
|

|
Crowding
|

|
Birth
|

|
Glider

|

|
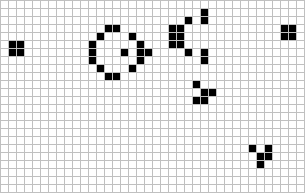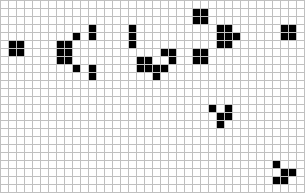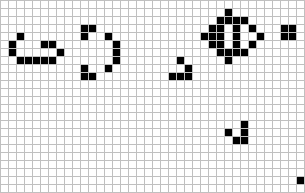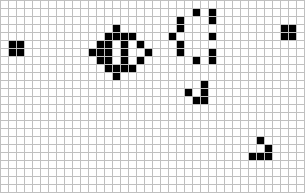
Loafer
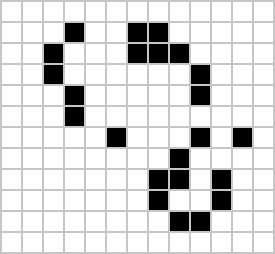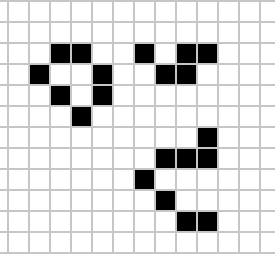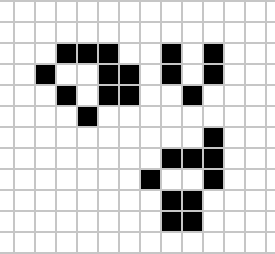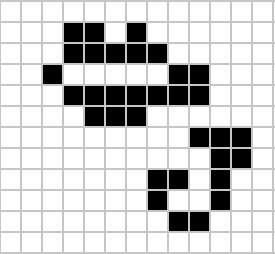
|

|

Laplace’s Gremlin

Philosophical Essay on Probabilities Laplace (1814) pg 5

Simulation System
Monolithic System
Service Oriented Architecture
Experiment, Analyze, Design
A Vision
We don’t know what science we’ll want to do in five years’ time, but we won’t want slower experiments, we won’t want more expensive experiments and we won’t want a narrower selection of experiments.
What do we want?
- Faster, cheaper and more diverse experiments.
Objective
A two order of magnitude increase in number of experiments run on supply chain three years’ time.
Statistical Emulation
Emulation
Emulation
Emulation
Emulation
Emulation
GPy and Emulation
Computation of
- Compute the expectation of the Branin function.
- Sample at 25 points on a grid.
- Compute the mean (Reiemann sum approximation).
Emulate and do MC Samples
Alternatively, we can fit a GP model and compute the integral of the best predictor by Monte Carlo sampling.
Branin Function Fit
Uncertainty Quantification
- History of interest, see e.g. McKay et al. (1979)
- The review:
- Random Sampling
- Stratified Sampling
- Latin Hypercube Sampling
- As approaches for Monte Carlo estimates
Random Sampling
Let the input values be a random sample from . This method of sampling is perhaps the most obvious, and an entire body of statistical literature may be used in making inferences regarding the distribution of .
Stratified Sampling
Using stratified sampling, all areas of the sample space of are represented by input values. Let the sample space of be partitioned into disjoint strata . Let represent the size of . Obtain a random sample , from . Then of course the sum to . If , we have random sampling over the entire sample space.
Latin Hypercube Sampling
The same reasoning that led to stratified sampling, ensuring that all portions of were sampled, could lead further. If we wish to ensure also that each of the input variables has all portions of its distribution represented by input values, we can divide the range of each into strata of equal marginal probability , and sample once from each stratum. Let this sample be , . These form the component, , in , . The components of the various ’s are matched at random. This method of selecting input values is an extension of quota sampling (Steinberg 1963), and can be viewed as a -dimensional extension of Latin square sampling (Raj 1968).
Emukit

Emukit
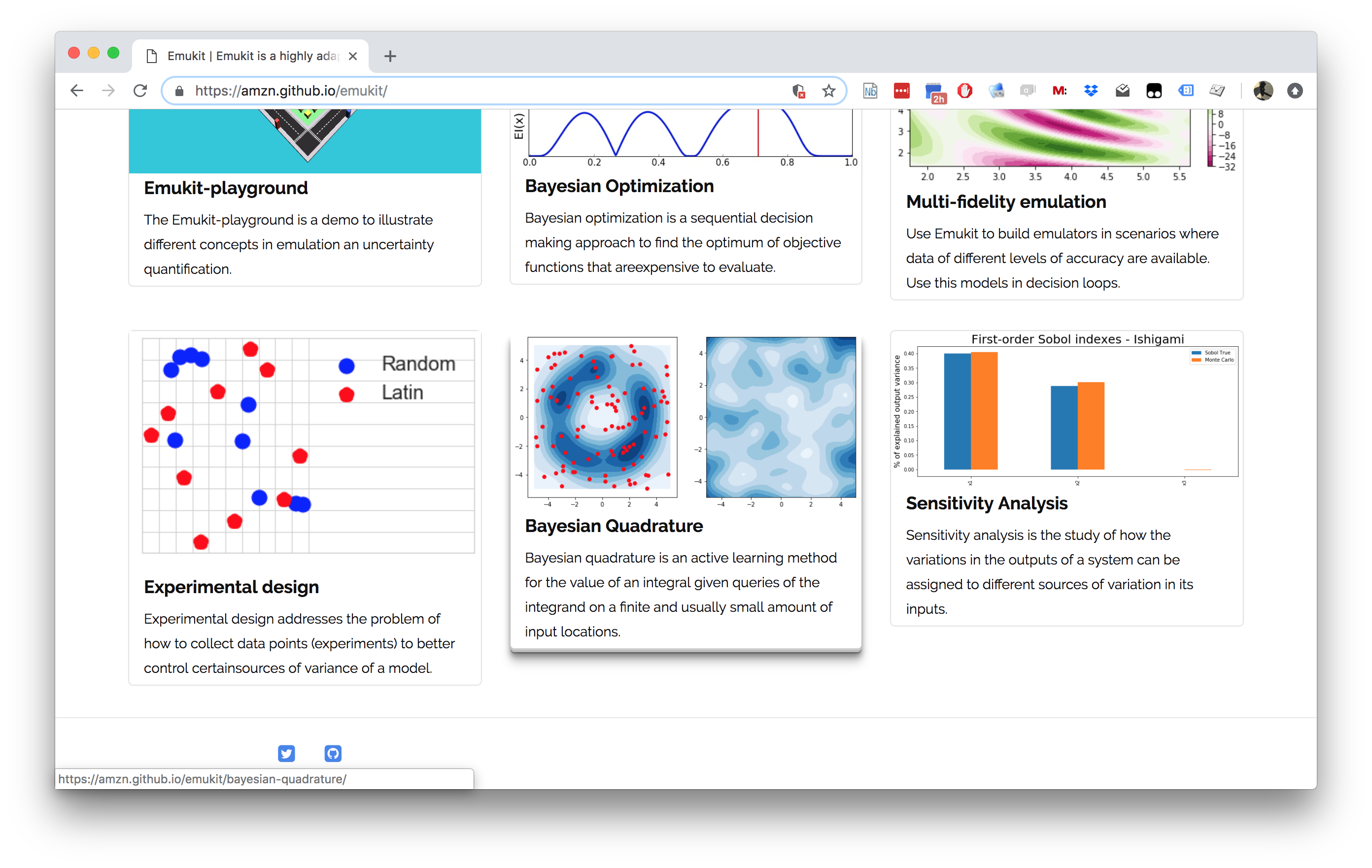
Emukit
- Led by: Javier Gonzalez and Andrei Paleyes
- Team: Mark Pullin, Maren Mahsereci, Alex Gessner, Aaron Klein, Henry Moss and David-Elias Künstle.
- Management: Cliff McCollum & Neil
- Available on Github
- Example sensitivity notebook, documentation https://emukit.readthedocs.io/en/latest/
Modular Design
Introduce your own surrogate models.
To building your own model see this notebook.
Emukit Playground
Work Adam Hirst, Software Engineering Intern and Cliff McCollum.
Tutorial on emulation.
Emukit Playground
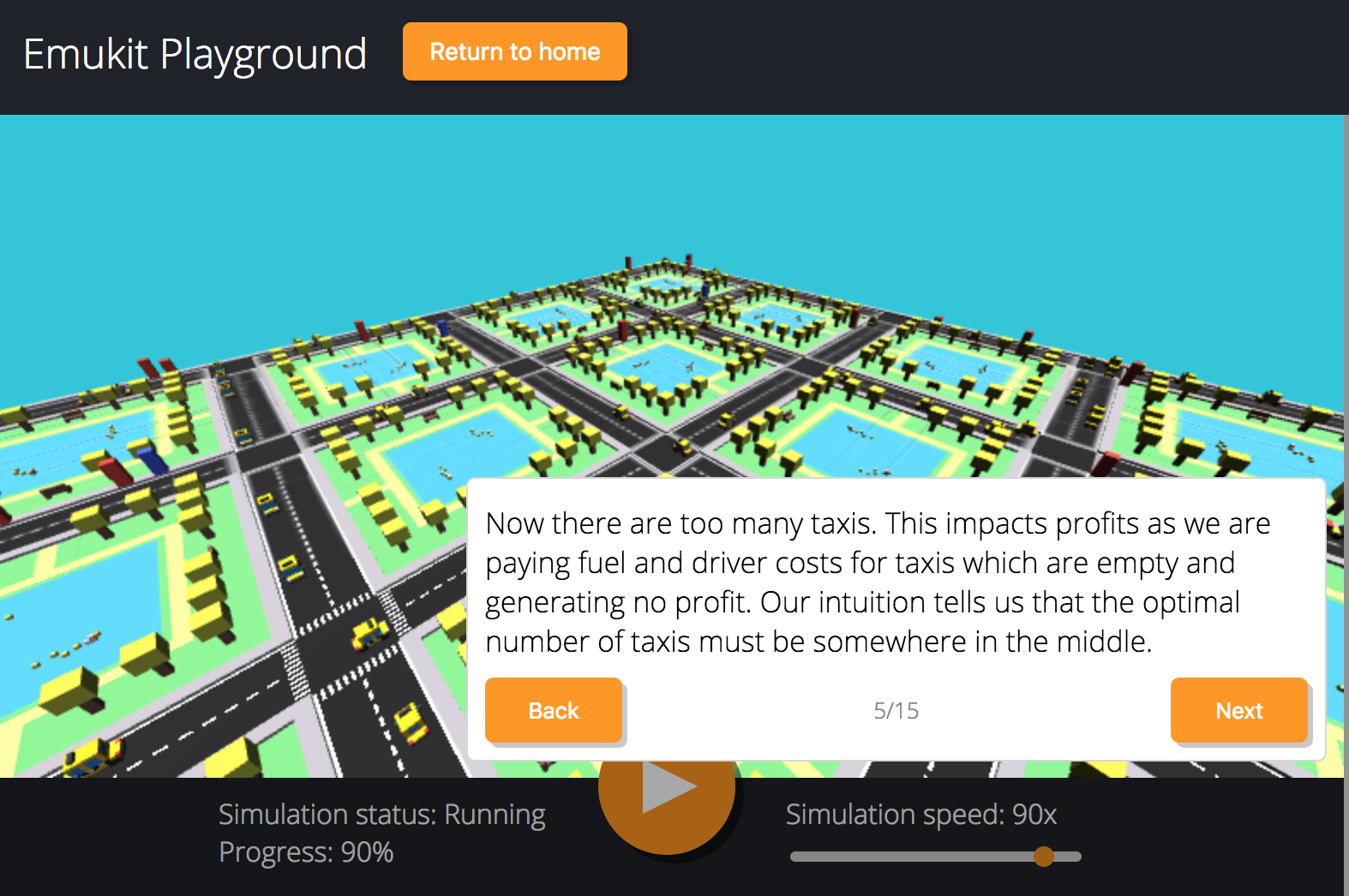
Emukit Playground
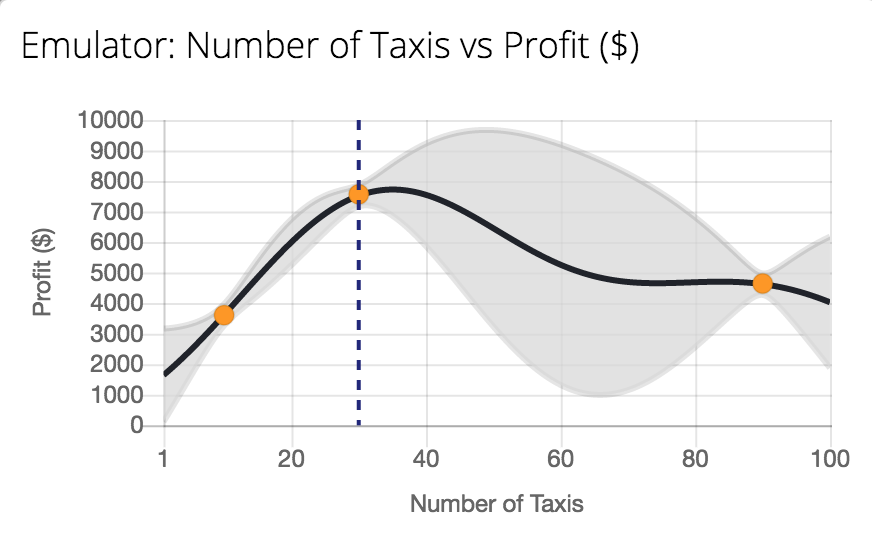
Emukit Sensitivity Analysis
A possible definition of sensitivity analysis is the following: The study of how uncertainty in the output of a model (numerical or otherwise) can be apportioned to different sources of uncertainty in the model input (Saltelli et al., 2004). A related practice is ‘uncertainty analysis,’ which focuses rather on quantifying uncertainty in model output. Ideally, uncertainty and sensitivity analyses should be run in tandem, with uncertainty analysis preceding in current practice.
In Chapter 1 of Saltelli et al. (2008)
Local Sensitivity
Global Sensitivity Analysis
Input Density
Hoeffding-Sobol Decomposition
Sobol Indices
Example: the Ishigami function
Ishigami Function
Total Variance
First Order Sobol Indices using Monte Carlo
Total Effects Using Monte Carlo
Computing the Sensitivity Indices Using the Output of a Model
Conclusions
- Sobol indices tool for explaining variance of output as coponents of input variables.
Catapult Simulation
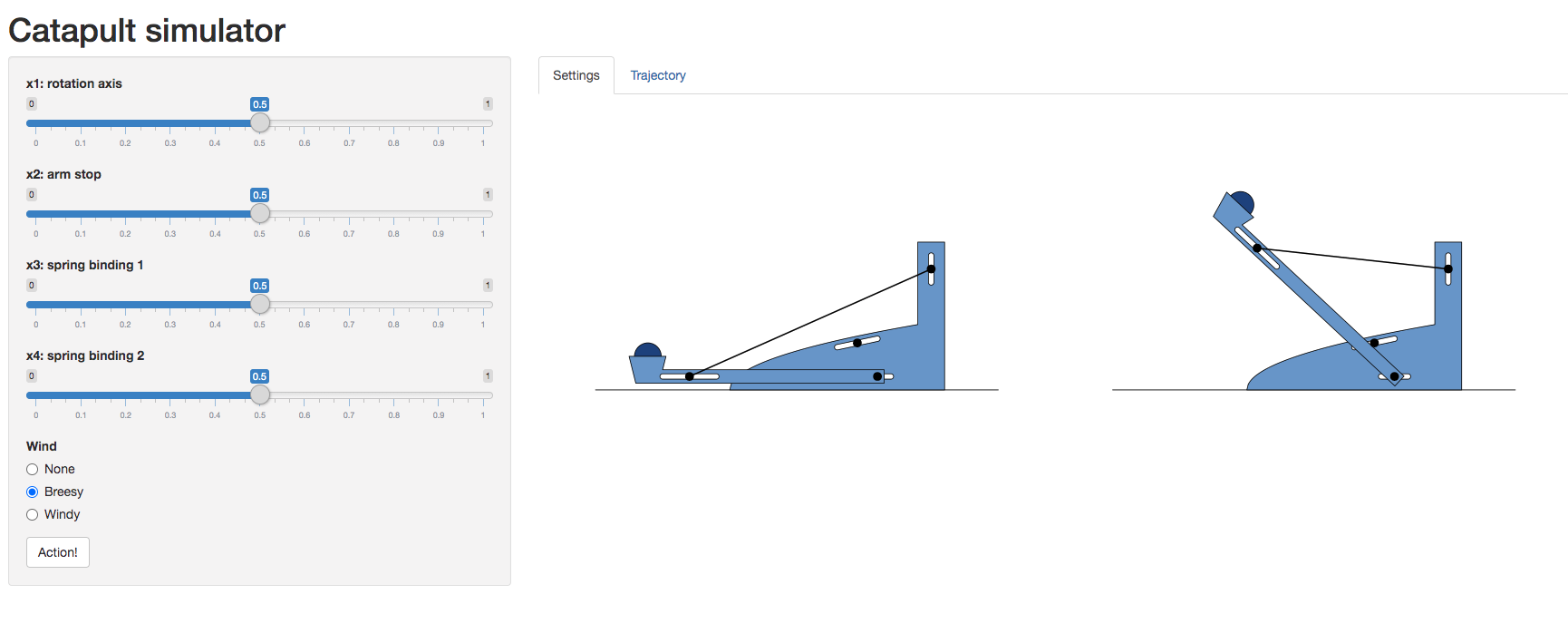
Experimental Design for the Catapult
- First build an experimental design loop.
- Start with model free design.
- Random design
- Latin hypercube sambling
- Sobol sequences
- Orthogonal design
Model Based Design
- Use integrated variance reduction.
- Try afterwards with uncertainty sampling.
Sensitivity Analysis of a Catapult Simulation
Thanks!
- twitter: @lawrennd
- podcast: The Talking Machines
- newspaper: Guardian Profile Page
- blog: http://inverseprobability.com